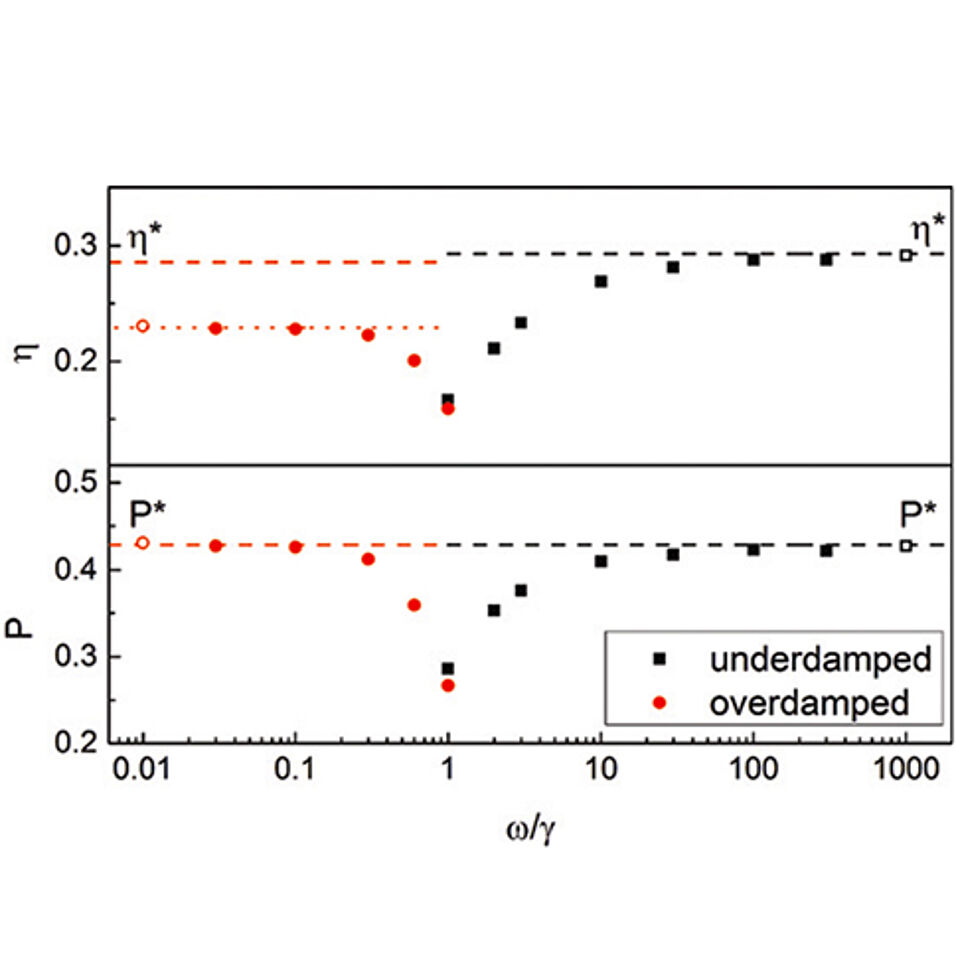
We investigate the performance of an underdamped stochastic heat engine, using the paradigmatic model of a harmonic oscillator with time-dependent frequency. We analytically determine the optimal protocol that maximizes the efficiency at fixed power. The maximum efficiency reduces to the Curzon-Ahlborn formula at maximum power and to the Carnot formula at zero power. We establish that the efficiency at maximum power is universally given by the Curzon-Ahlborn efficiency for weak damping. We further show that even small deviations from operation at maximum power results in a significantly increased efficiency.
Publication:
Underdamped Stochastic Heat Engine at Maximum Efficiency
Editors Choice
A. Dechant, N. Kiesel and Eric Lutz
Euro. Phys. Lett. 119, 50003 (2017), doi: 10.1209/0295-5075/119/50003.